Problema de cubos de Pepe Quintana
Este problema y las fotos están tomadas de la página de Belén Garrido http://pagina.de/papiroflexia.
¿Se forma un pentágono regular?
 Para que el "arco iris" forme un pentágono regular, si nos fijamos en el cubo verde de la base de la figura, el ángulo que forman los planos de los dos "besos" (el que se da con el cubo azul, a la izquierda, y con el cubo amarillo, a la derecha), debería ser de 72 grados.
Para que el "arco iris" forme un pentágono regular, si nos fijamos en el cubo verde de la base de la figura, el ángulo que forman los planos de los dos "besos" (el que se da con el cubo azul, a la izquierda, y con el cubo amarillo, a la derecha), debería ser de 72 grados.
 Pues bien, calculemos ese ángulo, basándonos en la siguiente foto, en donde el cubo verde de antes es, ahora, azul y las líneas rojas son parte de los dos planos de "beso" cuyo ángulo vamos a calcular.
Pues bien, calculemos ese ángulo, basándonos en la siguiente foto, en donde el cubo verde de antes es, ahora, azul y las líneas rojas son parte de los dos planos de "beso" cuyo ángulo vamos a calcular.
 Para ello, desplacemos los planos de "beso" paralelamente a sí mismos de modo que coincidan en la diagonal de la cara superior del cubo, es decir, cambiemos los dos besos por un fuerte achuchón.
Para ello, desplacemos los planos de "beso" paralelamente a sí mismos de modo que coincidan en la diagonal de la cara superior del cubo, es decir, cambiemos los dos besos por un fuerte achuchón.
Tenemos que ver si el ángulo diedro formado por los dos planos perfilados en rojo es de 72 grados.
Reduzcamos más la cuestión: por la simetría de la figura, cortemos el cubo azul por el plano vertical que pasa por la diagonal de la cara superior del cubo. Así, el ángulo que queremos determinar es la mitad del ángulo formado por el plano vertical y uno de los planos de "beso", el izquierdo, por ejemplo. Por tanto tenemos que ver si mide la mitad de 72, es decir, 36 grados.
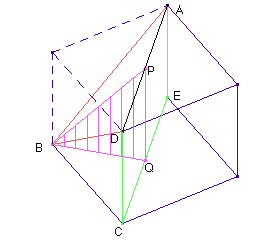 En el gráfico a la derecha los puntos A, B, C, D y E son todos vértices del cubo inicial. Los puntos P y Q son los puntos medios de las diagonales de las caras horizontales del cubo.
En el gráfico a la derecha los puntos A, B, C, D y E son todos vértices del cubo inicial. Los puntos P y Q son los puntos medios de las diagonales de las caras horizontales del cubo.
El ángulo diedro que queremos medir es el formado por el triángulo (rojo) ADB y el plano vertical ADCE (verde). La arista del diedro es la diagonal de color negro.
Para medir diedros hay que tomar perpendiculares a la arista. El segmento PB es perpendicular a la arista (se puede ver mirando el cubo desde arriba y horizontalmente) y el segmento PQ, también (por ser vertical). Así, el ángulo que queremos medir es exactamente el ángulo P en el triángulo rosa PBQ. Nuestro objetivo es determinar P y ver si mide 36 grados.
Lo que queda es fácil: tg P = BQ/PQ, ya que el ángulo Q es recto. Si el lado del cubo mide 1, la diagonal del cuadrado mediría 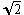 ; BQ es media diagonal y PQ mide igual que el lado del cubo, luego
; BQ es media diagonal y PQ mide igual que el lado del cubo, luego
tg P =
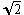
/2
El ángulo cuya tangente es 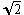 /2 mide 35,26 grados, por tanto
/2 mide 35,26 grados, por tanto
NO SE FORMA UN PENTÁGONO REGULAR
Entonces, ¿qué ángulo forman los cubos?

El ángulo rojo es el doble del que hemos determinado antes, es decir, 70,52 grados. El triángulo formado por las líneas rojas y la cara del cubo verde es isósceles. Como la suma de todos sus ángulos es de 180 grados, 180-70,52=109,48 es lo que miden conjuntamente los dos ángulos restantes (iguales entre sí) del triángulo. Pero eso mismo es lo que mide el ángulo que forman dos cubos adyacentes: 109,48 grados. Así que si los cubos fueran rígidos, el "arco iris" sería así:
Esta última imagen la ha hecho Pako, que me ha ayudado a "mirar correctamente" las figuras, y la ha fabricado con el programa de 3D, POV-Ray
La güebecilla del penta perfecto
Bar Xitai, 5 de octubre de 2001

 Para que el "arco iris" forme un pentágono regular, si nos fijamos en el cubo verde de la base de la figura, el ángulo que forman los planos de los dos "besos" (el que se da con el cubo azul, a la izquierda, y con el cubo amarillo, a la derecha), debería ser de 72 grados.
Para que el "arco iris" forme un pentágono regular, si nos fijamos en el cubo verde de la base de la figura, el ángulo que forman los planos de los dos "besos" (el que se da con el cubo azul, a la izquierda, y con el cubo amarillo, a la derecha), debería ser de 72 grados.
 Pues bien, calculemos ese ángulo, basándonos en la siguiente foto, en donde el cubo verde de antes es, ahora, azul y las líneas rojas son parte de los dos planos de "beso" cuyo ángulo vamos a calcular.
Pues bien, calculemos ese ángulo, basándonos en la siguiente foto, en donde el cubo verde de antes es, ahora, azul y las líneas rojas son parte de los dos planos de "beso" cuyo ángulo vamos a calcular.
 Para ello, desplacemos los planos de "beso" paralelamente a sí mismos de modo que coincidan en la diagonal de la cara superior del cubo, es decir, cambiemos los dos besos por un fuerte achuchón.
Para ello, desplacemos los planos de "beso" paralelamente a sí mismos de modo que coincidan en la diagonal de la cara superior del cubo, es decir, cambiemos los dos besos por un fuerte achuchón.
 En el gráfico a la derecha los puntos A, B, C, D y E son todos vértices del cubo inicial. Los puntos P y Q son los puntos medios de las diagonales de las caras horizontales del cubo.
En el gráfico a la derecha los puntos A, B, C, D y E son todos vértices del cubo inicial. Los puntos P y Q son los puntos medios de las diagonales de las caras horizontales del cubo.
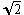 ; BQ es media diagonal y PQ mide igual que el lado del cubo, luego
; BQ es media diagonal y PQ mide igual que el lado del cubo, luego
