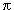 radianes es media circunferencia
radianes es media circunferencia
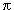 radianes
radianes
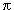 radianes
radianes
Usemos como unidad de medida de ángulos el radián, ya que las cuentas resultan mucho más fáciles:
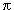 radianes es media circunferencia
radianes es media circunferencia
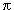 radianes
radianes
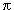 radianes
radianes
Omitiendo la unidad a partir de ahora, el radián, recalculemos los ángulos que intervienen en un pentágono regular. Llamo  a la quinta parte de
a la quinta parte de 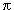 , es decir,
, es decir,  =
=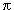 /5.
/5.
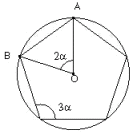 En el triángulo AOB, el ángulo O es la quinta parte de la circunferencia, es decir, 2
En el triángulo AOB, el ángulo O es la quinta parte de la circunferencia, es decir, 2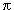 /5, que es lo mismo que 2
/5, que es lo mismo que 2 . Como el triángulo es isósceles, los ángulos A y B miden lo mismo y, como el total A+B+O debe ser
. Como el triángulo es isósceles, los ángulos A y B miden lo mismo y, como el total A+B+O debe ser 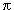 , entonces A+B juntos miden el resto hasta
, entonces A+B juntos miden el resto hasta 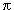 . Decir que
. Decir que  es la quinta parte de
es la quinta parte de 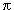 es lo mismo que decir que
es lo mismo que decir que
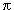 = 5
= 5 y así A+B debe ser 3
y así A+B debe ser 3 .
Mirando el pentágono regular, lo que mide un ángulo cualquiera es justo la suma A+B, es decir, 3
.
Mirando el pentágono regular, lo que mide un ángulo cualquiera es justo la suma A+B, es decir, 3 .
.
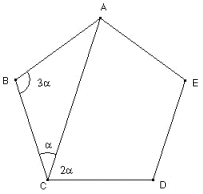 Tracemos ahora la diagonal AC y veamos cuánto mide el ángulo C visto en el triángulo ABC, que es isósceles. Fácil: el total de ángulos suma
Tracemos ahora la diagonal AC y veamos cuánto mide el ángulo C visto en el triángulo ABC, que es isósceles. Fácil: el total de ángulos suma 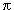 , que es lo mismo que 5
, que es lo mismo que 5 ; el ángulo B mide 3
; el ángulo B mide 3 , luego tanto A como C miden
, luego tanto A como C miden  .
Vemos también que como el ángulo C visto ahora en el pentágono mide 3
.
Vemos también que como el ángulo C visto ahora en el pentágono mide 3 y la parte de él que está en el triángulo ABC mide
y la parte de él que está en el triángulo ABC mide  , entonces el resto mide 2
, entonces el resto mide 2 .
.
Si dibujamos la diagonal AD tenemos una división simétrica del pentágono. Así, el triángulo formado por las dos diagonales y la base del pentágono es isósceles.
En la figura que sigue vemos todos los ángulos con su medida.
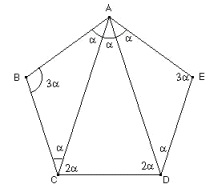
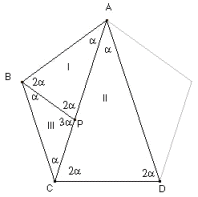 Sobre la diagonal AC hagamos lo siguiente: desde el punto A marcamos una longitud igual que el lado del pentágono regular, resultando de ello el punto P.
Sobre la diagonal AC hagamos lo siguiente: desde el punto A marcamos una longitud igual que el lado del pentágono regular, resultando de ello el punto P.
El triángulo I es isósceles ya que el lado AP es igual a AB por construcción. El triángulo II es isósceles por la simetría del pentágono regular. En ambos triángulos, I y II, el ángulo desigual mide  según vimos. Si en dos triángulos isósceles coinciden la medida del ángulo desigual (el opuesto al lado desigual), necesariamente coinciden las medidas de los otros ángulos y, en consecuencia, son semejantes. En nuestro caso la medida de los restantes ángulos es 2
según vimos. Si en dos triángulos isósceles coinciden la medida del ángulo desigual (el opuesto al lado desigual), necesariamente coinciden las medidas de los otros ángulos y, en consecuencia, son semejantes. En nuestro caso la medida de los restantes ángulos es 2 .
.
¿Qué se ve en el triángulo III de vértices BPC?
El ángulo P de dicho triángulo junto con el ángulo P del triángulo I forman un ángulo llano, es decir, 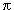 . Como en I mide 2
. Como en I mide 2 , en III medirá lo que falte para
, en III medirá lo que falte para 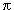 =5
=5 , es decir, 3
, es decir, 3 . El ángulo C en el triángulo III sabíamos ya que medía
. El ángulo C en el triángulo III sabíamos ya que medía  . Por tanto, el restante ángulo del triángulo III medirá lo que falte para
. Por tanto, el restante ángulo del triángulo III medirá lo que falte para 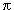 , o sea,
, o sea,  (esto último también lo podemos deducir del hecho de que el ángulo B del pentágono mide 3
(esto último también lo podemos deducir del hecho de que el ángulo B del pentágono mide 3 ; este ángulo queda dividido en dos partes, una, en el triángulo I y que mide 2
; este ángulo queda dividido en dos partes, una, en el triángulo I y que mide 2 y otra, en el III, debiendo de medir, por tanto, la diferencia a 3
y otra, en el III, debiendo de medir, por tanto, la diferencia a 3 , es decir,
, es decir,  ) . En consecuencia, el triángulo III resulta ser isósceles por tener dos ángulos iguales y, así, resulta que los lados BP y PC miden lo mismo.
) . En consecuencia, el triángulo III resulta ser isósceles por tener dos ángulos iguales y, así, resulta que los lados BP y PC miden lo mismo.
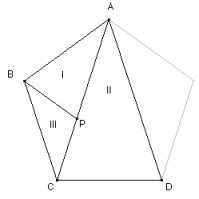 La semejanza de los triángulos I y II significa la proporcionalidad de sus lados homólogos
La semejanza de los triángulos I y II significa la proporcionalidad de sus lados homólogos
| I | II | |
| lado desigual | BP | CD |
| lado repetido | AB | AC |
En lenguaje algebraico: BP/AB=CD/AC, pero refiriéndonos sólo a los segmentos que hay sobre la diagonal, podemos cambiar CD y AB por AP (hemos construído AP de modo que mida lo que el lado del pentágono regular), y sustituir BP por PC ya que vimos que el triángulo III es isósceles: PC/AP=AP/AC
Pero esto último no es más que decir que en el segmento
AC, dividido por P en dos partes, la parte menor es a la mayor como ésta es al total, es decir, AP es la sección áurea de AC, o bien
Problema de cubos de Pepe Quintana
Bar Xitai (Última modificación, 5 de octubre de 2001)